余姚麻将里的七小对牌型收益模拟

前段时间玩了两次余姚麻将，规则里带有地方麻将常见的癞子规则（癞子牌被叫做龙牌）。边打边学的时候我了解到，七小对/七对子在这个规则里是最大的番种之一，也就是和牌的人可以把其他三家的点数全部赢到手里（每人开局发100点，任何一人把这100点输光这局就算结束）。根据之前打立直麻将的经验，七对子并不是一个很难和的牌，再加上有龙牌辅助，我当时就觉得它应该是余姚麻将的版本答案。可惜的是那两天有意试着做了几次，最多只实现了一次听牌。打完之后好奇我的猜测是否正确，写了个模拟脚本来检验七对子的收益有多高。

假设某玩家A在第一轮摸牌的时候发现手里的牌包含若干个对子和若干张龙牌，直接开始闷头做七对子。那么这把牌只有三种结局，一是玩家A和了牌，显然A的收益期望为300点，二是其他玩家和牌，此时A的收益期望为某个负值，三则是没有任何人和牌，A的收益期望为0。对于第二和第三种情况，综合考虑点炮、别家自摸、有人开杠这些因素，估计A的损失大约为20点，可能有些高估。

在上述条件下，假设在余姚麻将中平均的和牌轮数为X，A在此轮或之前和牌的概率为Y，那么A做七对子的收益即为300×Y-20×(1-Y)。X难以计算，先搁置。Y则可以通过模拟来统计。模拟的过程中，A的策略是把手牌中在场上出现次数最多的那张打出，以此增加和牌概率。为了简化，模拟中除了A以外的三个玩家都是无情的摸到哪张就打哪张的机器，也不会吃碰杠。

模拟代码如下：

import random


times_to_test = 10000
list_tiles_all = [j for j in range(34) for i in range(4)]
list_round = []
# 余姚麻将一共136张牌，垒完长城后一张牌要翻开来指示龙牌，它和被它压住的牌是不能被摸走的，那么第21轮只有两个玩家能摸牌，第22轮用来记录A在这一把没有和牌的情况
list_result = [[] for _ in range(23)]
for number_pair, number_loong in ((2, 1), (1, 2), (4, 0), (3, 1), (4, 1), (3, 2)):
    print(number_pair, number_loong)
    list_round.append({each: 0 for each in range(1, 23)})
    for _ in range(times_to_test):

        # 选定编号33是龙牌指示牌，编号0是龙牌，为了方便起见，假设龙牌指示牌和它压住的牌在牌堆最末尾
        list_tiles = list_tiles_all[:]
        list_tiles.remove(33)
        list_pairs = []
        list_loong = [list_tiles.pop(0) for _ in range(number_loong)]
        list_single = []
        while len(list_pairs) + number_loong + len(list_single)< 14:                  
            if each_tile := random.choice(list_tiles):
                if len(list_pairs) < 2 * number_pair and (each_tile < 33 or each_tile not in list_pairs):
                    for _ in range(2):
                        list_pairs.append(each_tile)
                        list_tiles.remove(each_tile)
                elif each_tile not in list_single:
                    list_single.append(each_tile)
                    list_tiles.remove(each_tile)
        dict_tiles_shown = {each: 0 for each in range(34)}

        random.shuffle(list_tiles)
        # 把A的手牌初始化后，从牌堆中删去其余三人的手牌，以及牌堆最末尾被龙牌指示牌压住的牌
        # 摸牌顺序随机，各自摸13张牌后在第一轮到A再摸一张，这时可能已经有人出过牌了，要先把它们记下，然后再出牌
        order = random.randint(0, 3)
        list_tiles = list_tiles[39:-1]
        for _ in range(order):
            dict_tiles_shown[list_tiles.pop(0)] += 1
        list_single.remove(sorted(list_single, key=lambda x: dict_tiles_shown[x],  reverse=True)[0])

        number_count = order
        number_round = 1
        win = False
        while list_tiles:
            number_count += 1
            each_tile = list_tiles.pop(0)
            dict_tiles_shown[each_tile] += 1
            if number_count % 4 == order:
                number_round += 1
                if each_tile == 0:
                    list_loong.append(each_tile)
                elif each_tile in list_single:
                    list_pairs.append(each_tile)
                    list_pairs.append(each_tile)
                    list_single.remove(each_tile)
                else:
                    list_single.append(each_tile)
                if len(list_loong) >= len(list_single):
                    win = True
                    break
                list_single.remove(sorted(list_single, key=lambda x: dict_tiles_shown[x],  reverse=True)[0])

        list_round[-1][number_round if win else 22] += 1

    probability_all = 0
    for i in range(1, 22):
        probability = list_round[-1][i] / times_to_test
        probability_all += probability
        list_result[i] += [probability, probability_all, probability_all * 300 - (1 - probability_all) * 20]

for each_round in list_result[1:22]:
    print(' '.join([str(each_value) for each_value in each_round]))
input()

以上是对A的起始手牌（第一轮摸完牌的状态）中包含2对+1龙/1对+2龙/4对+0龙/3对+1龙/4对+1龙/3对+2龙的这几种情况的模拟，模拟结果如下：

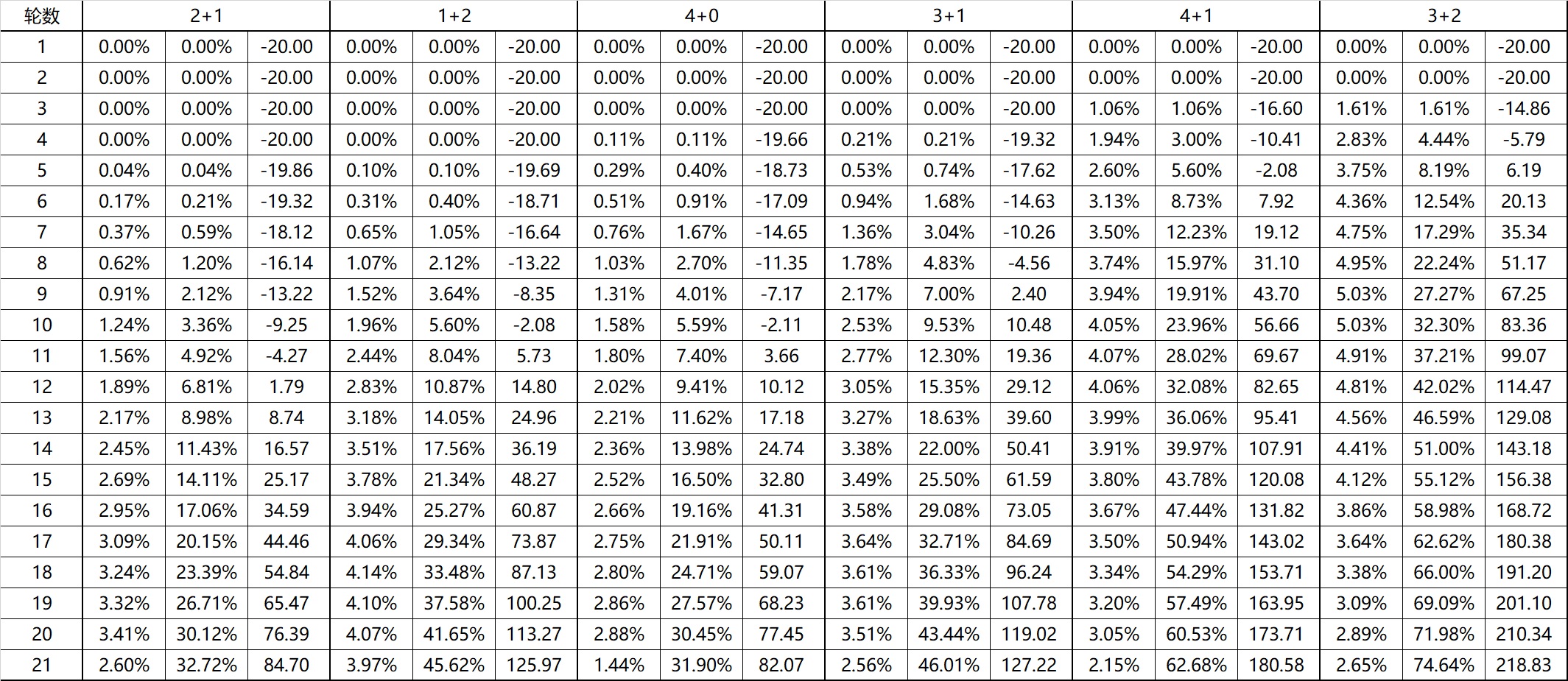
每种情况下的第一列是A在该轮的和牌概率，第二列是在该轮或之前和牌的概率，也就是前面提到的Y，第三列是X取整后为该轮数（显然X不会是一个整数）时A的收益期望。从这张图可以看到，前三种情况下，A的收益期望为正的前提是X大于12/11/11，后三种情况则只要求X大于9/6/5。

在立直麻将里，X一般在11到13之间，余姚麻将因为和牌更容易，X会稍小些，可能会在9和11之间。也就是说，只要初始手牌包含3对+1龙/4对+1龙/3对+2龙，那么做七对的收益就是划算的，和我的猜想基本一致，只不过我高估了4对+0龙的收益。当然，这个模拟并不严谨，图一乐罢了2333