水排序谜题
在群里看到有人玩一个叫水排序的游戏,看他们发的截图觉得这个游戏应该可以写一个脚本来解。搜了下发现有人做过一个求解的网页,还有位大佬写了一个启发式搜索的算法。前者没有给出源码,只能看到压缩后的不可读版,后者又太过复杂,于是想试试能不能自己写一个。
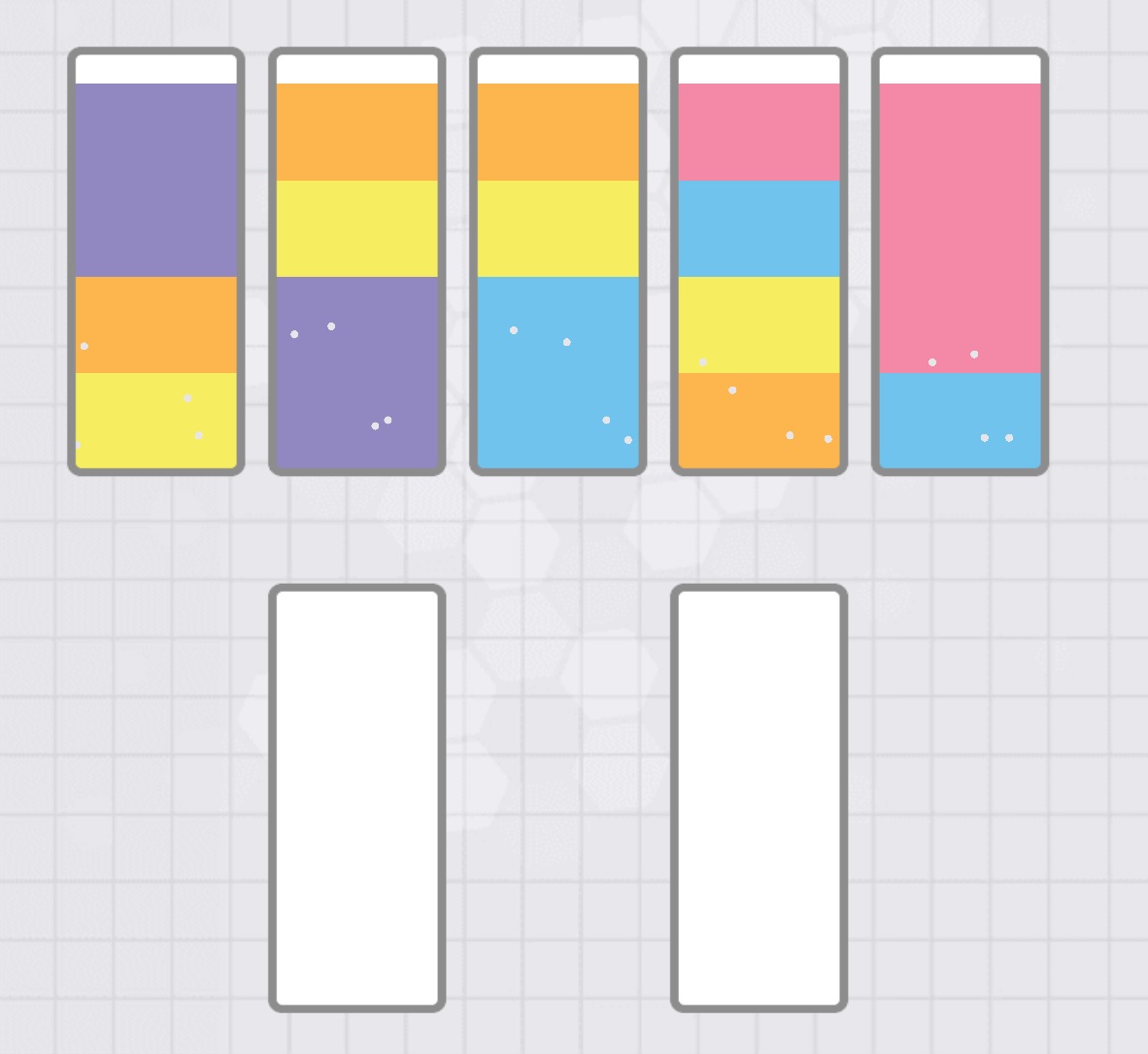
这个游戏找到一个网页版的,上图是游戏画面的截图。只看这张图也能基本猜到游戏规则:每种颜色的水的数量是4,杯子的容量也是4,杯子数量大于水的颜色数量;不同颜色的水互相隔离且不会互换位置(可以理解成一块固体物质);游戏目的是通过互相倒水将所有相同颜色的4个水整理到同个杯子里;倒水时,除非目标杯子是空的,当前杯子和目标杯子里最上方的水的颜色必须一样,且只能倒出这个颜色的水。
对于这个问题,最先想到的就是穷举法。虽然目测步数比较多,但每一步的可选项都不多,每一步都尽量减少局面复杂度的话应该是可以比较快地解出来的。
那么如何制定策略呢?试着玩了几局之后,发现它和经典游戏蜘蛛纸牌有些类似,首先要尽可能留出空杯,其次是要优先把数量更多的同色水聚集起来。
于是试着根据这两个策略写解法。期间遇到一个问题:假设杯子A最上方是2格X颜色的水且没有空,杯子B最上方是1格X颜色的水和1格空,如何防止AB轮流倒1格水给对方导致死循环?第一反应是记录倒水的顺序,拒绝前一步操作的反向操作。但是再一想就发现这样无法避免三个杯子之间的循环或者多种颜色之间的交错循环。仔细思考后,我认为上述这类局面下本就不该在AB杯之间倒X颜色的水,因为它们并不会减少局面的复杂度。所以策略中还需增加一条:只有目标杯子中的空位能容纳当前杯子可以倒出的最大水量时,才进行倒水操作。由于担心这条策略会在极端情况下把题目卡住,我设计了一个小型的被卡住的局面,发现其实它是可解的,于是推测更大型的局面下可选项更多,解法更不会被阻塞,由此认为这条策略是安全的。
最终的代码如下:
class Bottle:
def __init__(self, index, colors=None):
self.index = index
self.colors = [None] * 4 if colors is None else colors
self.number_colors = 0
self.number_empty = 0
self.color_last = None
self.number_same_color = 0
self.check()
def check(self):
colors = [each_color for each_color in self.colors if each_color]
self.number_colors = len(colors)
self.number_empty = 4 - self.number_colors
self.color_last = colors[-1] if colors else None
self.number_same_color = 0
while self.color_last and self.number_same_color < self.number_colors and colors[-self.number_same_color - 1] == self.color_last:
self.number_same_color += 1
def pour(self, target, number_to_pour):
for i_c in range(number_to_pour):
self.colors[self.number_colors - 1 - i_c] = None
target.colors[target.number_colors + i_c] = self.color_last
self.check()
target.check()
class Bottles:
def __init__(self):
self.bottles = []
self.number_bottles = 0
index = 0
print('输入:')
while True:
colors = input().split()
if colors:
if len(colors) == 4:
index += 1
self.bottles.append(Bottle(index, [None if each_color == '0' else each_color for each_color in colors]))
else:
print('此次输入有误,请重新输入')
continue
else:
break
frequency = {}
for each_bottle in self.bottles:
for each_color in each_bottle.colors:
frequency[each_color] = frequency.get(each_color, 0) + 1
for each in frequency:
if (each is None and frequency[each] % 4) or (each and frequency[each] != 4):
print(each, frequency[each])
print((each if each else '空') + '的数量为' + str(frequency[each]) + ',不符合规则,请重试')
return
self.number_bottles = len(self.bottles)
def solve():
global bottles, steps, failure
options = []
for bottle_i in bottles.bottles:
for bottle_j in bottles.bottles:
if bottle_i is not bottle_j and ((bottle_i.color_last == bottle_j.color_last and bottle_i.number_same_color <= bottle_j.number_empty) or bottle_j.number_empty == 4) and not (bottle_i.number_colors == bottle_i.number_same_color and bottle_j.number_empty == 4):
number_to_pour = bottle_i.number_same_color
options.append([bottle_i, bottle_j, number_to_pour, (bottle_i.number_colors == bottle_i.number_same_color) * 100 + number_to_pour * 10 + bottle_j.number_same_color])
if len(options) == 0:
failure += 1
return False
for each_try in sorted(options, key=lambda each_option: -each_option[3]):
steps.append([each_try[0].index, each_try[1].index])
each_try[0].pour(each_try[1], each_try[2])
if sum([(each_bottle.number_empty == 4 or each_bottle.number_same_color == 4) for each_bottle in bottles.bottles]) == bottles.number_bottles:
return True
else:
result_next_try = solve()
if result_next_try:
return True
else:
del steps[-1]
each_try[1].pour(each_try[0], each_try[2])
return False
while True:
bottles = Bottles()
if bottles.number_bottles:
break
steps = []
failure = 0
solve()
print('steps:', len(steps))
print('failure:', failure)
print('\n'.join([str(each_step[0]) + '→' + str(each_step[1]) for each_step in steps]))
input()
测试用例1:
4 3 2 1
5 5 4 1
7 6 13 3
3 6 8 1
9 2 13 7
12 6 10 9
8 7 12 2
2 11 12 13
7 10 11 3
5 11 4 4
1 9 5 10
8 9 8 10
6 11 12 13
0 0 0 0
0 0 0 0
0 0 0 0
测试用例2:
0 0 0 0
0 0 0 0
1 12 3 2
10 12 5 8
7 8 7 11
2 7 5 10
6 5 6 8
1 11 6 2
10 11 3 4
3 11 9 9
5 4 3 4
12 4 8 9
9 6 7 10
2 1 12 1